从“猫和老鼠”题解看博弈题型

原题链接：点击这里访问

猫和老鼠题干
#

两位玩家分别扮演猫和老鼠，在一张无向图上进行游戏，两人轮流行动。

图的形式是：graph[a] 是一个列表，由满足 ab 是图中的一条边的所有节点 b 组成。

老鼠从节点 1 开始，第一个出发；猫从节点 2 开始，第二个出发。在节点 0 处有一个洞。

在每个玩家的行动中，他们必须沿着图中与所在当前位置连通的一条边移动。例如，如果老鼠在节点 1 ，那么它必须移动到 graph[1] 中的任一节点。

此外，猫无法移动到洞中（节点 0）。

然后，游戏在出现以下三种情形之一时结束：

如果猫和老鼠出现在同一个节点，猫获胜。
如果老鼠到达洞中，老鼠获胜。 = 如果某一位置重复出现（即，玩家的位置和移动顺序都与上一次行动相同），游戏平局。

给你一张图 graph ，并假设两位玩家都都以最佳状态参与游戏：

如果老鼠获胜，则返回 1；
如果猫获胜，则返回 2；
如果平局，则返回 0 。

示例 1：

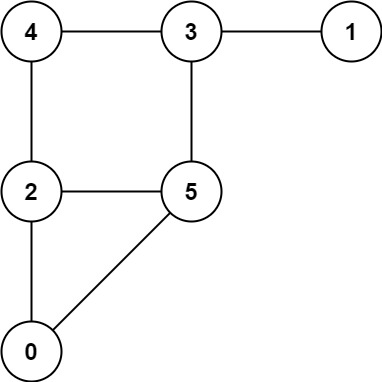
输入：graph = [[2,5],[3],[0,4,5],[1,4,5],[2,3],[0,2,3]] 输出：0 示例 2：

输入：graph = [[1,3],[0],[3],[0,2]] 输出：1

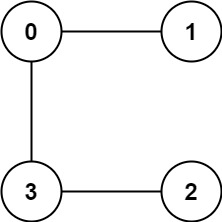
提示：

3 <= graph.length <= 50
1 <= graph[i].length < graph.length
0 <= graph[i][j] < graph.length
graph[i][j] != i
graph[i] 互不相同
猫和老鼠在游戏中总是可以移动

博弈前置知识
#

显然此题和博弈有关。先回忆最简单的博弈：NIM 游戏。

给定 N 堆石子，第 i 堆有 ai 个石子。

两名玩家轮流行动，每次在一堆石子中取若干个，不能不取，最后不能取的人输。

原题链接：点击这里访问

简单来说，在公平博弈中，己方的最优策略是通过将对方引入其必败状态来确保胜利。

核心思想是，在假设双方都采用最优策略的情况下：

如果从某个状态可以到达至少一个对方必败状态，那么该状态对于己方就是必胜的。
反之，如果无法到达任何对方必败状态，则该状态对己方就是必败的。
如果游戏存在平局，则无法在确认必胜或必负的情况就是平局。

对于该前置内容，我在24年初写过一道蓝桥杯的题，连接贴在下面可以参考：

原题链接：点击这里访问

灭鼠先锋是一个老少咸宜的棋盘小游戏，由两人参与，轮流操作。

灭鼠先锋的棋盘有各种规格，本题中游戏在两行四列的棋盘上进行。游戏的规则为：两人轮流操作，每次可选择在棋盘的一个空位上放置一个棋子，或在同一行的连续两个空位上各放置一个棋子，放下棋子后使棋盘放满的一方输掉游戏。

小蓝和小乔一起玩游戏，小蓝先手，小乔后手。小蓝可以放置棋子的方法很多，通过旋转和翻转可以对应如下四种情况：

XOOO XXOO OXOO OXXO 
OOOO OOOO OOOO OOOO

其中 O 表示棋盘上的一个方格为空，X 表示该方格已经放置了棋子。

请问，对于以上四种情况，如果小蓝和小乔都是按照对自己最优的策略来玩游戏，小蓝是否能获胜。如果获胜，请用 V 表示，否则用 L 表示。请将四种情况的胜负结果按顺序连接在一起提交。

24年题解如下

#include <bits/stdc++.h>
using namespace std;
bool check(string s){//判断是否只有一个O
   int cnt = 0;
   for(auto i : s){
       cnt += i=='O';
   }
   return cnt == 1;
}
unordered_map<string, bool>mp;
bool dfs(string s){
   if(mp.count(s))return mp[s];
   if(check(s)){//当当前状态只有一个O时标记为必败态
       mp[s] = false;
       return false;
   }

   // 核心思路是只有遍历能到达一个必败态，此态就是必胜的（两人都是最优策略）
   // 如果一个必败态都无法到达，此态就是必败的
   // 进行记忆化搜素
   
   // 放置一个
   for(int i = 0; i < s.size(); i ++){
       if(s[i] == 'O'){
           string tmp = s;
           tmp[i] = 'X';
           if(dfs(tmp) == false){
               mp[s] = true;
               return true;
           }
       }
   }
   // 放置两个
   for(int i = 0; i < s.size(); i ++){
       if(s[i] == 'O' && s[i+1] == 'O' && i != 3){
           string tmp = s;
           tmp[i] = 'X';
           tmp[i+1] = 'X';
           if(dfs(tmp) == false){
               mp[s] = true;
               return true;
           }
       }
   }
   mp[s] = false;
   return false;
}
int main() {
   	dfs("OOOOOOOO");
   	dfs("XOOOOOOO");
   	dfs("OXOOOOOO");
   	dfs("XXOOOOOO");
   	dfs("OXXOOOOO");
   	cout << mp["OXXOOOOO"] << endl;
   	return 0;
}

记忆化搜索
#

一般而言，博弈问题可以转化为搜索问题。显然在博弈过程中会有大量重复子问题，因此往往会引入记忆化搜索。

对于该题，很容易思考到搜索的前两个参数：猫位置与鼠位置。而第三个参数则有两种可能的写法，即 bool 类型表示现在是哪方的回合，以及 int 类型表示当前第几回合。

而初始状态为：

老鼠成功进洞，即 dp[0][j][1] = 1 （贪心可知，老鼠赢的下一回合一定是猫的回合）
猫捉到老鼠，即 dp[i][i][1] = 2 dp[i][i][0] = 2

如果想用 bool 类型表示回合，就又引出了新的问题。在无法确定回合数的情况下，如果不加上其他限制，对于平局会进入无限循环的搜索。

但是对于 int 类型表示回合数，在此题的时间复杂度是不够的：

在本题中，猫和鼠的数据范围都是 n 。如果第三个参数为上述的 int 行，其上界为： \( 2 \times n^2 \) 则搜索状态为 \( O(n^4) \)，而此题的初始状态数上述提到过了是 n ，因此总复杂度为： \( O(n^5) \) 不能满足时间要求。

根据上面的分析，此题的问题变为：在使用 bool 表示当前是谁的回合时，如何避免出现无限循环的搜索并尽可能剪枝。

对于回合数作为第三个参数时的官方题解如下：

class Solution {
public:
    const int MOUSE_TURN = 0, CAT_TURN = 1;
    const int DRAW = 0, MOUSE_WIN = 1, CAT_WIN = 2;
    vector<vector<int>> graph;
    vector<vector<vector<int>>> degrees;
    vector<vector<vector<int>>> results;

    int catMouseGame(vector<vector<int>>& graph) {
        int n = graph.size();
        this->graph = graph;
        this->degrees = vector<vector<vector<int>>>(n, vector<vector<int>>(n, vector<int>(2)));
        this->results = vector<vector<vector<int>>>(n, vector<vector<int>>(n, vector<int>(2)));
        queue<tuple<int, int, int>> qu;

        for (int i = 0; i < n; i++) {
            for (int j = 1; j < n; j++) {
                degrees[i][j][MOUSE_TURN] = graph[i].size();
                degrees[i][j][CAT_TURN] = graph[j].size();
            }
        }
        for (int node : graph[0]) {
            for (int i = 0; i < n; i++) {
                degrees[i][node][CAT_TURN]--;
            }
        }
        for (int j = 1; j < n; j++) {
            results[0][j][MOUSE_TURN] = MOUSE_WIN;
            results[0][j][CAT_TURN] = MOUSE_WIN;
            qu.emplace(0, j, MOUSE_TURN);
            qu.emplace(0, j, CAT_TURN);
        }
        for (int i = 1; i < n; i++) {
            results[i][i][MOUSE_TURN] = CAT_WIN;
            results[i][i][CAT_TURN] = CAT_WIN;
            qu.emplace(i, i, MOUSE_TURN);
            qu.emplace(i, i, CAT_TURN);
        }
        while (!qu.empty()) {
            auto [mouse, cat, turn] = qu.front();
            qu.pop();
            int result = results[mouse][cat][turn];
            vector<tuple<int, int, int>> prevStates = GetPrevStates(mouse, cat, turn);
            for (auto & [prevMouse, prevCat, prevTurn] : prevStates) {
                if (results[prevMouse][prevCat][prevTurn] == DRAW) {
                    bool canWin = (result == MOUSE_WIN && prevTurn == MOUSE_TURN) || (result == CAT_WIN && prevTurn == CAT_TURN);
                    if (canWin) {
                        results[prevMouse][prevCat][prevTurn] = result;
                        qu.emplace(prevMouse, prevCat, prevTurn);
                    } else if (--degrees[prevMouse][prevCat][prevTurn] == 0) {
                        int loseResult = prevTurn == MOUSE_TURN ? CAT_WIN : MOUSE_WIN;
                        results[prevMouse][prevCat][prevTurn] = loseResult;
                        qu.emplace(prevMouse, prevCat, prevTurn);
                    }
                }
            }
        }
        return results[1][2][MOUSE_TURN];
    }

    vector<tuple<int, int, int>> GetPrevStates(int mouse, int cat, int turn) {
        vector<tuple<int, int, int>> prevStates;
        int prevTurn = turn == MOUSE_TURN ? CAT_TURN : MOUSE_TURN;
        if (prevTurn == MOUSE_TURN) {
            for (int & prev : graph[mouse]) {
                prevStates.emplace_back(prev, cat, prevTurn);
            }
        } else {
            for (int & prev : graph[cat]) {
                if (prev != 0) {
                    prevStates.emplace_back(mouse, prev, prevTurn);
                }
            }
        }
        return prevStates;
    }
};

拓扑排序前置知识
#

此题说是用到拓扑排序并不准确，更应该说是用到拓扑排序的“ 入度表 ”的思想。

入度表 记录 每个节点被指向的次数。
使用队列处理 入度为 0 的节点。
不断删除已处理的节点，更新 入度表。
若无法遍历所有节点，则存在环。
时间复杂度 O(n + m)，适用于有向无环图（DAG）。

对于该拓扑排序前置知识，可以参考下面：

任务拓扑排序
#

一个工程被分解成n个子任务，编号为0至n-1。要完成整个工程需要完成所有的子任务。其中一些子任务必须先于另外一些子任务被完成。给定各子任务之间的先后关系，请编写程序给出一个合理的任务完成顺序，若工程不可行，程序亦能识别。

输入第一行为两个整数n和e，均不超过100。n表示子任务数。接下来e行，表示已知的两个子任务间的先后关系，每行为两个整数a和b，表示任务a必须先于任务b完成。

若工程不可行（一些子任务以自己为先决条件），输出“unworkable project”；若工程可行，输出为1行整数，每个整数后一个空格，为n个子任务的编号，表示子任务的完成顺序，如果有多种可能的顺序，则输出字典序最小者。

注：字典序，即对象在字典中的顺序。对于两个数字序列，从第一个数字开始比较，当某一个位置的数字不同时，该位置数字较小的序列，字典序较小，例如1 2 3 9比1 2 4 5小，1 2 8 9比1 2 10 3小。

样例1：
3 2
0 1
1 2
0 1 2 
样例2：
3 3
0 1
1 2
2 0
unworkable project
ANSWER
#
#include <bits/stdc++.h>
using namespace std;
int main() {
   int n, m;
   cin >> n >> m;
   vector<vector<int>> graph(n);
   vector<int> inDegree(n, 0); // 记录每个节点的入度
   // 读取边信息
   for (int i = 0; i < m; i++) {
       int from, to;
       cin >> from >> to;
       graph[from].push_back(to);
       inDegree[to]++; // 目标节点的入度增加
   }
   // 小顶堆（优先队列）保证字典序最小
   priority_queue<int, vector<int>, greater<int>> q;
   // 将所有入度为 0 的节点入队
   for (int i = 0; i < n; i++) {
       if (inDegree[i] == 0) {
           q.push(i);
       }
   }
   vector<int> topoOrder; // 记录拓扑排序结果
   while (!q.empty()) {
       int node = q.top();
       q.pop();
       topoOrder.push_back(node);

       for (int neighbor : graph[node]) {
           inDegree[neighbor]--; // 删除当前节点的出边
           if (inDegree[neighbor] == 0) { // 若入度变为 0，则加入队列
               q.push(neighbor);
           }
       }
   }
   // 如果排序结果中的节点数小于总节点数，说明有环
   if (topoOrder.size() < n) {
       cout << "unworkable project" << endl;
   } else {
       for (int node : topoOrder) {
           cout << node << " ";
       }
   }
   return 0;
}

动态规划
#

那么在这道题中，如果为所有状态添加一个入度表，就可以做到上述的剪枝。

同样的，我们选择自顶向下，初始状态为：

老鼠成功进洞，即 result[0][j][1] = 1 （贪心可知，老鼠赢的下一回合一定是猫的回合）
猫捉到老鼠，即 result[i][i][1] = 2 result[i][i][0] = 2
其他状态设置为 0，即平局。

而对于入度的初始化为：

degree[i][j][0] = len(graph[i])
degree[i][j][1] = len(graph[j])
degree[i][j][1] -= 1 if j in graph[0] （猫不能在洞里）

那么状态转移可以理解为：

从最终状态遍历每一个前置状态：
- 若遍历到该前置状态的必胜态，则使其入度为零。
- 如没遍历到必胜态，则每次遍历使得其入度减一，知道其度为零，则设置其为必败态。
将已经确定必败或必胜的状态加入 queue 中， BFS 遍历其前置状态。
该转移没有遍历到的状态即平局状态。

当然此题还有些细节需要注意，可以看题解中的注释:

class Solution:
    def catMouseGame(self, graph: List[List[int]]) -> int:
        n = len(graph)
        queue = deque()
        # 状态为 degree[i][j][k] 表示:
        # 老鼠在 i , 猫在 j, 谁先手为 k (0 表示老鼠回合，1 表示猫回合)
        degree = [[[0, 0] for _ in range(n)] for _ in range(n)]
        result = [[[0, 0] for _ in range(n)] for _ in range(n)]
        def init():
            for i in range(n):
                for j in range(1, n):
                    degree[i][j][0] = len(graph[i])
                    degree[i][j][1] = len(graph[j])
                    
            # 猫不能在洞里，所以要减去这种特殊情况
            for i in range(n):
                for j in graph[0]:
                    degree[i][j][1] -= 1

            for i in range(n):
                for j in range(1, n):
                    if i == 0:
                        result[i][j][1] = 1
                        # result[i][j][0] = 1
                        queue.append([i, j, 1])
                        # queue.append([i, j, 0])
                    elif i == j:
                        result[i][j][1] =2
                        result[i][j][0] =2
                        queue.append([i, j, 1])
                        queue.append([i, j, 0])
        init()

        # 检查前一个状态是否已经能被确定
        def preCheck(preMouse, preCat, preTurn, result_state):
            if result[preMouse][preCat][preTurn] != 0:
                return
            # 如果下一个状态能赢，则直接确定为赢
            win = True if result_state == 1 + preTurn else False
            if win:  # 如果能赢，则入度直接归零
                result[preMouse][preCat][preTurn] = result_state
                queue.append((preMouse, preCat, preTurn))
                degree[preMouse][preCat][preTurn] = 0  # 避免重复处理
            else:
                degree[preMouse][preCat][preTurn] -= 1
                if degree[preMouse][preCat][preTurn] == 0:
                    result[preMouse][preCat][preTurn] = 2 - preTurn
                    queue.append((preMouse, preCat, preTurn))

        # queue 中都是已经确定结果的状态
        while queue:
            mouse, cat, turn = queue.popleft()
            result_state = result[mouse][cat][turn]
            preTurn = 1 - turn  # 换手

            if preTurn == 0:  # 前一个回合是老鼠
                for preMouse in graph[mouse]:
                    preCheck(preMouse, cat, preTurn, result_state)
            else:  # 前一个回合是猫
                for preCat in graph[cat]:
                    if preCat == 0:
                        continue
                    preCheck(mouse, preCat, preTurn, result_state)
        
        return result[1][2][0]