机器学习 - 应试笔记

• 课程内容主要来自于斯坦福 cs229。

• 在应试之外，此博客对机器学习入门也能提供一定的参考。

• 部分内容直接来自 PPT 讲义截图，可能对阅读产生不便，请谅解。

• 本博客分为三部分，请自行在目录跳转。

  • 知识点内容总结
  • 考试复习重点
  • 考试数学推导重点（手写）

第01章-绪论

#

推理期->知识期->学习期

符号主义学习:

✓决策树：以信息论为基础，最小化信息熵

✓基于逻辑的学习：用逻辑进行知识表示，通过修改扩充逻辑表达式对数据进行归纳

连接主义学习:

✓神经网络和深度学习

统计学习:

✓支持向量机及核方法

✓2006年卡耐基梅隆大学成立第一个“机器学习系”系主任–机器学习奠基人之一T. Mitchell教授

新的方向：集成学习 强化学习 迁移学习 深度学习

第02章-线性回归

#

假设函数 / 拟合函数：

#

重点看其中的参数定义

代价函数

#

绝对误差，平方和误差

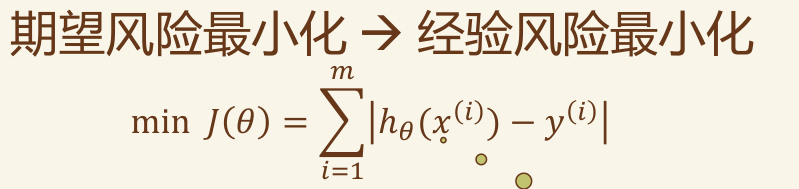
线性回归示例

#

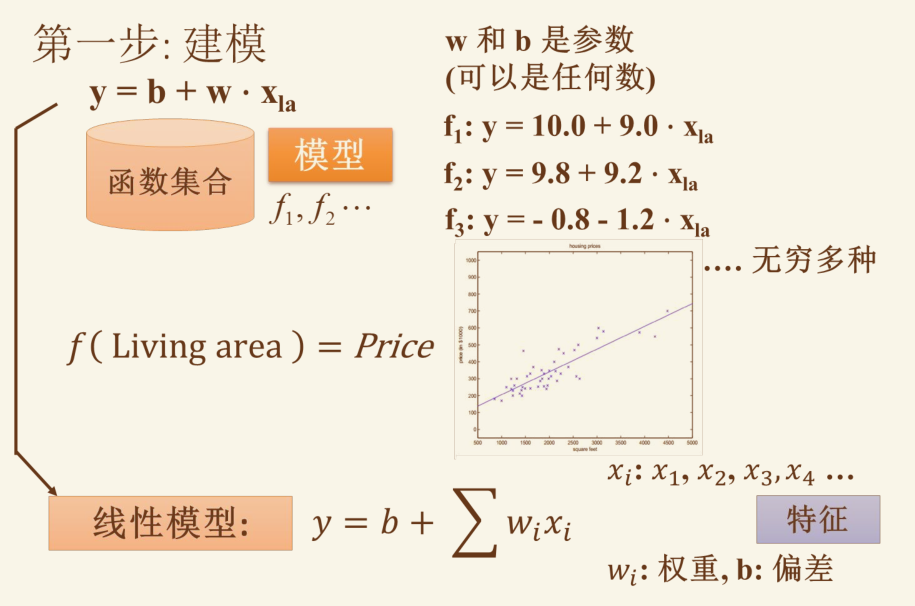
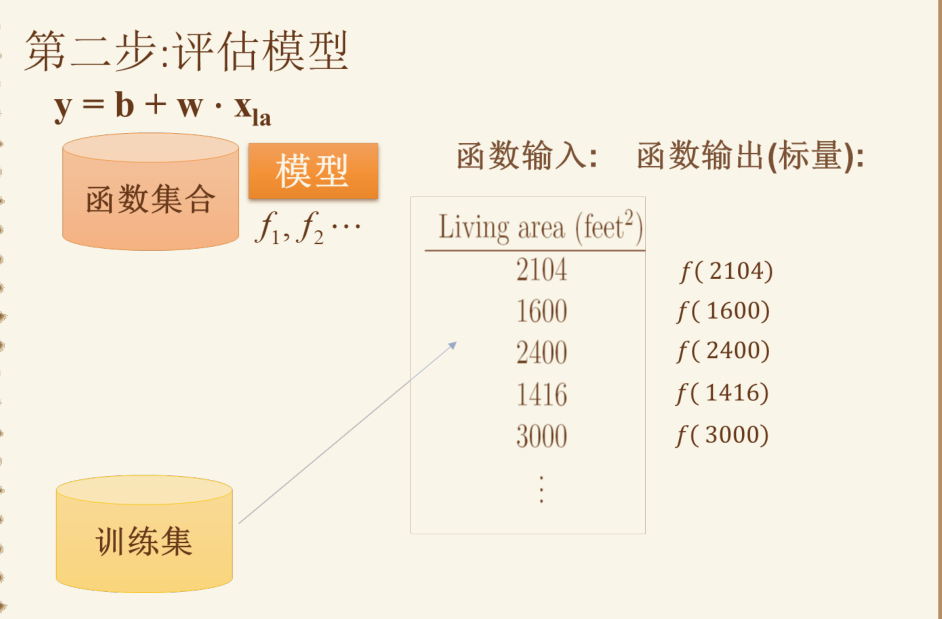
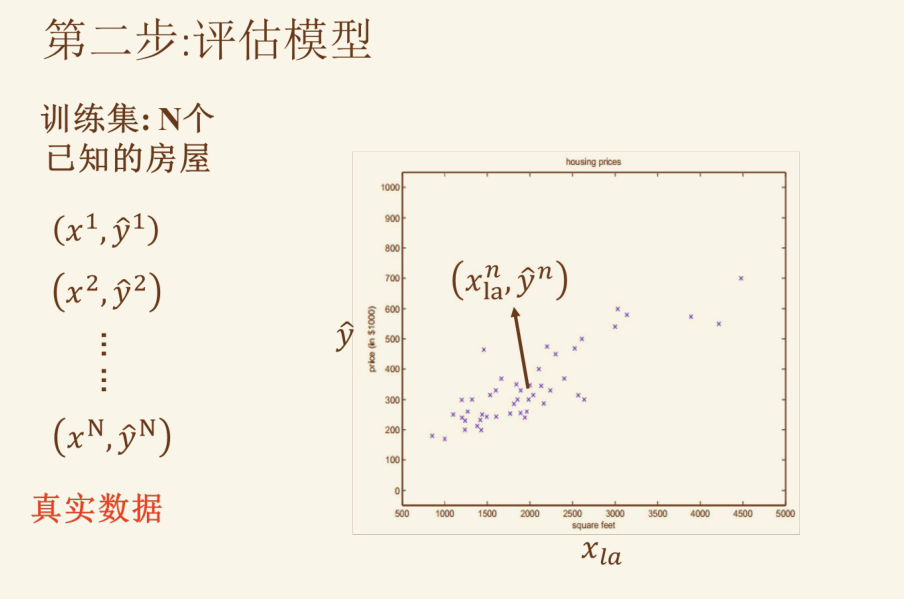
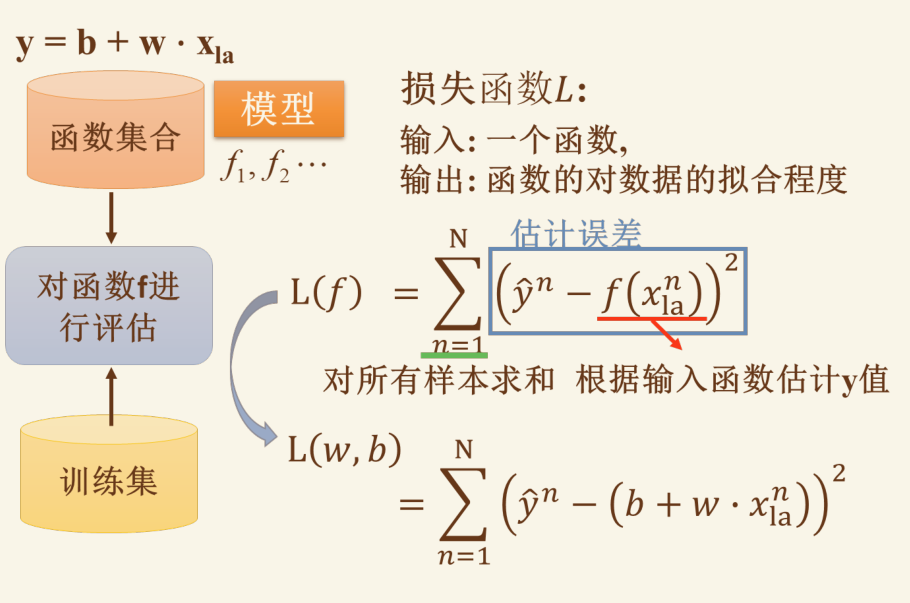
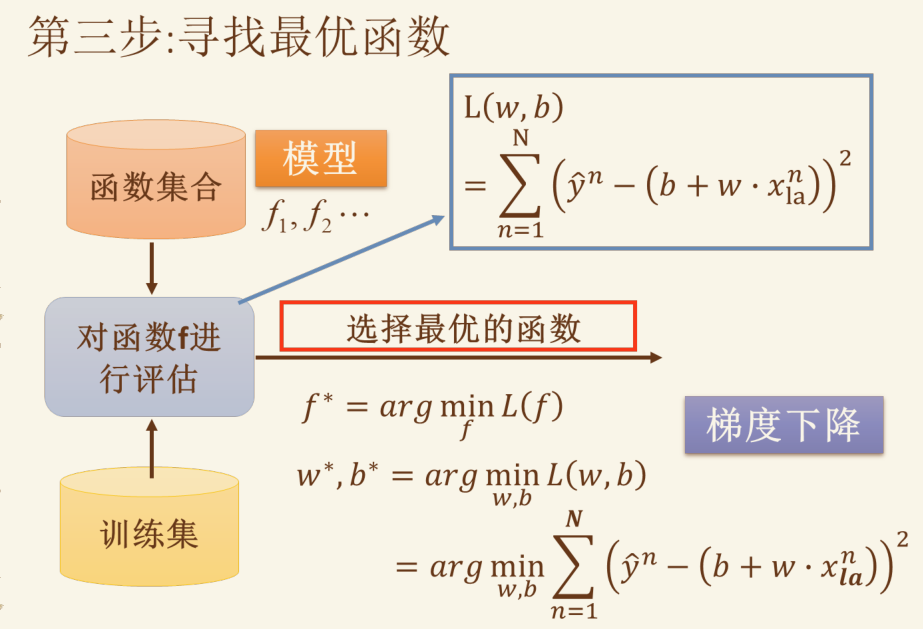
注意上图最后一个公式挺重要的

特征规范化

#

（维度特征 - 均值）/ 标准差

x1 = (x1 - mean(x1)) / std(x1)

用来将尺度缩放到 -1 到 1 之间

需要注意的是，特征缩放并不是一件很严格的事，他只是为了优化梯度下降效率的一个技巧，换句话说，没有明确的标准来规定每个向量的数据尺度应该是多少，从经验上来讲，[-1, 1]的尺度可以接受1/3到30左右的尺度偏差

目标函数（最小二乘法）

#

注意对比目标函数和代价函数，基本上目标函数就是多了个min

一般而言，1/2应该为1/2m，使得函数值和数据量有关。

这里的 2m 可以看做是方便后续计算而多写了一个 2 ，因为损失函数总会对某个变量求导，而恰好可以与平方项的求导结果抵消

最小二乘法的正规方程

#

正规方程是直接用梯度和目标函数反推参数的方法，和梯度下降并列。直接计算出每个参数，精准且无需超参数但计算量大。

梯度下降法

#

关键因子计算：

#

即线性回归下的梯度下降可以简化公式

即参数 θi 的梯度 = 误差值 * xi

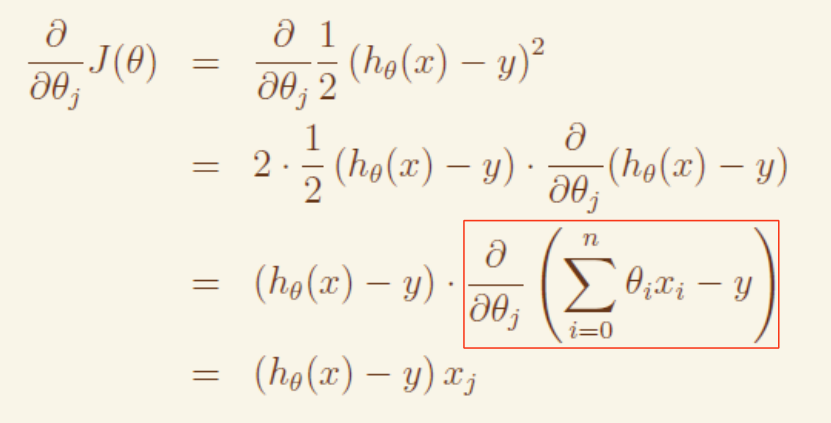
BGD vs SGD

#

解决的是协调多样本梯度下降，其中 SGD 更常用

学习率

#

正规方程 vs 梯度下降

#

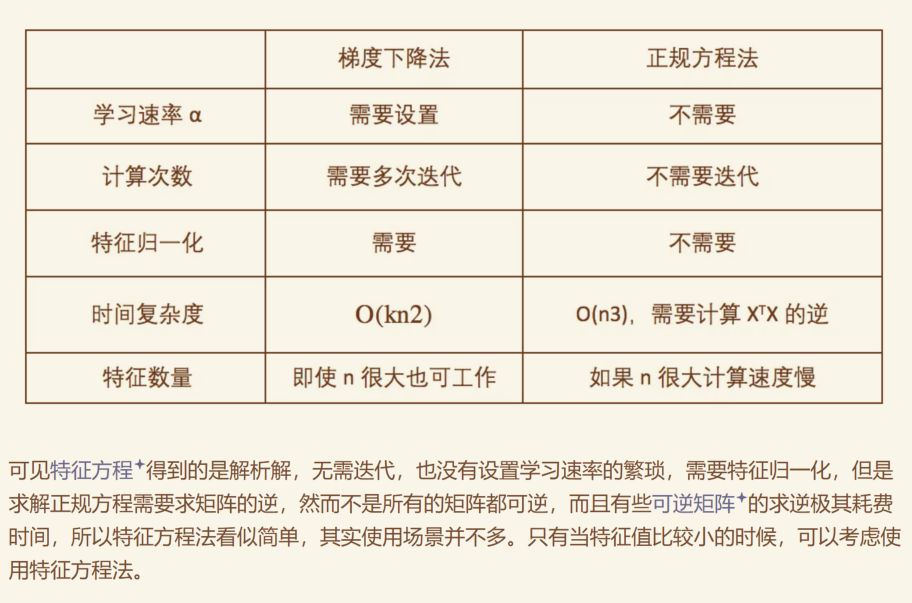
局部加权线性回归

#

每项中添加 w 作为系数，一般用高斯核：

欠拟合、过拟合、正则化

#

样本离群点：指显著偏离总体分布的异常数据点，可能影响统计分析结果。

欠拟合（Underfitting）

• 欠拟合发生在模型对训练数据的学习不足，无法很好地捕捉训练数据的规律，也无法在训练集和测试集上表现出良好的性能。
• 这通常是因为模型的复杂度太低，无法表示训练数据中的模式。

过拟合（Overfitting）

• 过拟合发生在模型对训练数据学习得过多，甚至学习到了训练数据中的噪声和细节，从而失去了对新数据的泛化能力。
• 过拟合的模型在训练集上的表现非常好，但在测试集上的表现较差。

正则化（Regularization）

定义

• 正则化是一种用于防止过拟合的技术，通过在损失函数中加入额外的约束项（正则化项），限制模型的复杂度，从而提高模型的泛化能力。

原理

• 在模型的损失函数中加入正则化项，通过对模型参数施加惩罚，限制参数的大小或稀疏性，使模型避免过度拟合训练数据。

• L1正则化（Lasso Regularization）

  • 在损失函数中加入参数的 L1 范数（即参数的绝对值之和）。

  • 优点：会使一些参数变为 0，从而实现特征选择，得到稀疏模型。

  • 

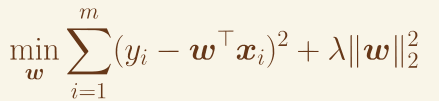
  L2正则化（Ridge Regularization）

  • 在损失函数中加入参数的 L2 范数（即参数的平方和）。

  • 优点：不会使参数变为 0，但能有效减小参数的值，防止过拟合。

  • 正则化项：（下图L1 L2 反了2）

    

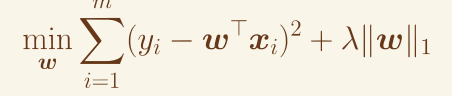
  Elastic Net 正则化

  • L1 和 L2 正则化的结合，综合两者的优点。

第03章-逻辑回归

#

激活函数

#

• 单位阶跃函数

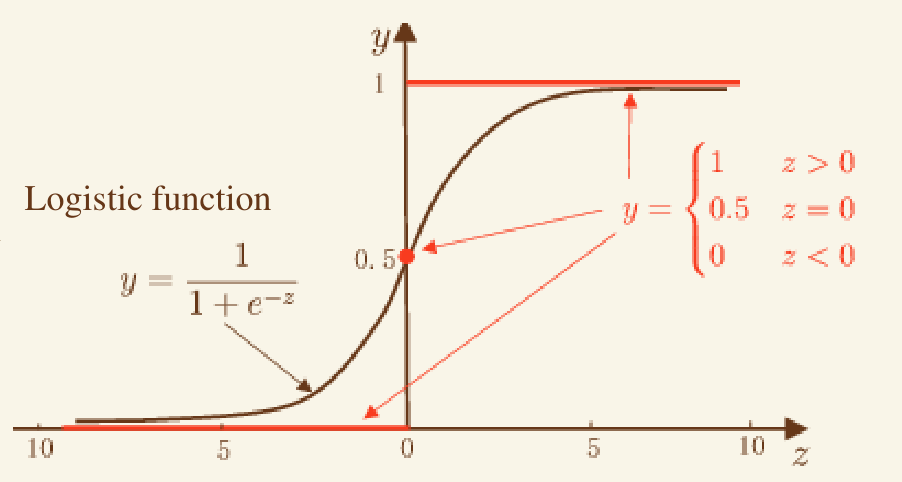
• sigmoid

  

  

  

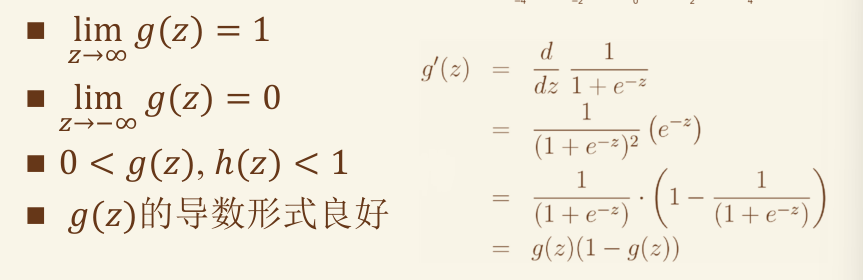
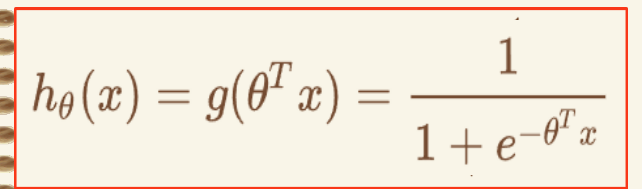
逻辑回归的概率假设

#

对数几率变换

#

Odds = 事件发生的概率 / 事件不发生的概率

Odds = P(A) / [1 - P(A)]

似然函数

#

注意 PPT 上的形式中 i 在右上角，并加括号。

梯度法 最大似然函数

#

线性回归梯度法的关键因子为：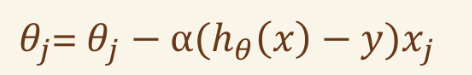

形式上和逻辑回归的梯度上升维持相似：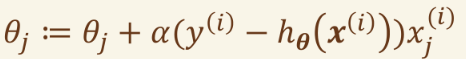

其假设函数对比如下：

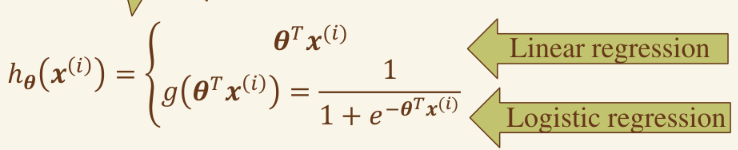
牛顿法 极大似然函数

#

牛顿法和梯度法对比

#

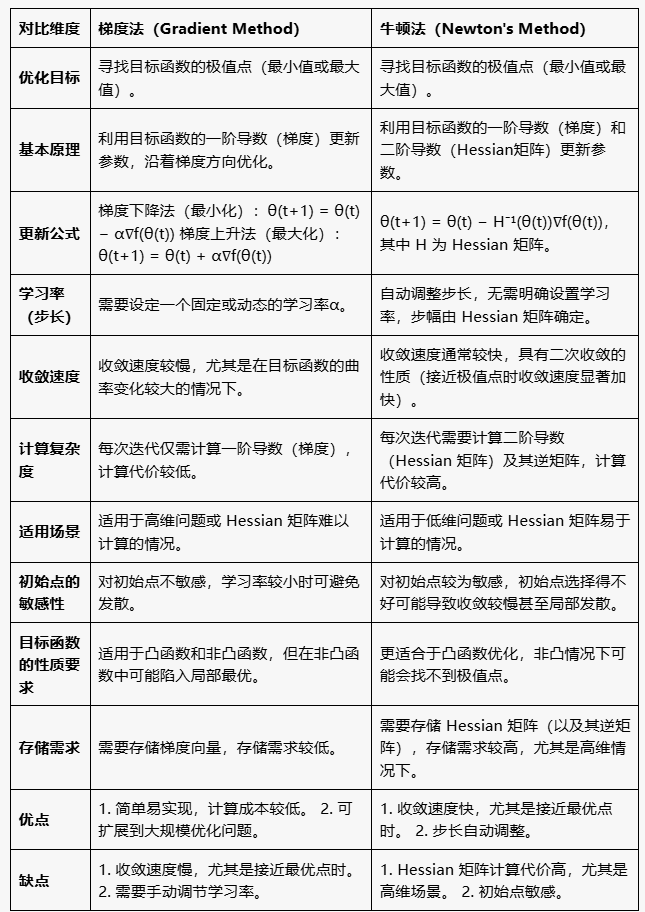
模型评估方法

#

• 训练集 (training): • 用于学习的数据集合 • 通常50 - 80 %的数据
• 验证集(validation):（平时很少使用到） • 用于设置和调整超参数的数据集合 • 通常10 - 20 %的数据
• 测试集(test): • 一组用于评估完整训练模型性能的数据 • 在评估测试集性能之后，不能进一步调优模型 • 通常10 - 30 %的数据

样本集的划分

1. 留出法

留出法是对数据集进行一次性划分，将数据分为训练集和测试集，用于评估模型性能。

关键点：

• 分层采样：在划分数据集时，按类别比例（或其他特征）进行分层采样，确保训练集和测试集的分布与原始数据一致。

• 数据划分比例

  • 通常将数据的 2/3 到 4/5 用于训练，剩余部分用于测试（验证）。

• 测试集的样本数量建议大于 30，以保证评估结果的可靠性。

• 优点

  • 简单直接，计算开销小。

• 缺点

  • 测试集划分的结果可能会受到数据分割方式的影响，存在一定随机性。

• 训练数据量较少时，模型可能无法充分学习。

---

2. 交叉验证法

交叉验证法是一种更稳定和常用的模型验证方法，通过多次划分和训练来全面评估模型性能。

关键点：

• K 折交叉验证

  • 将数据集分为 K 个互斥的子集，每次将其中 1 个子集作为验证集，其余 K-1 个子集作为训练集。

• 这个过程重复 K 次，确保每个子集都被用作验证集一次。

  • 通常取 K=10（10 折交叉验证），以获得较好的性能评估。

• 分层采样

  • 和留出法类似，分层采样确保每个子集中的数据分布与原始数据一致。

• K=样本数（留一法 Leave-One-Out）

  • 当 K 等于数据集样本数时，每次只用 1 个样本作为验证集，其余样本作为训练集，这种方法称为 留一法。

• 留一法适合小规模数据集，但计算开销较大。

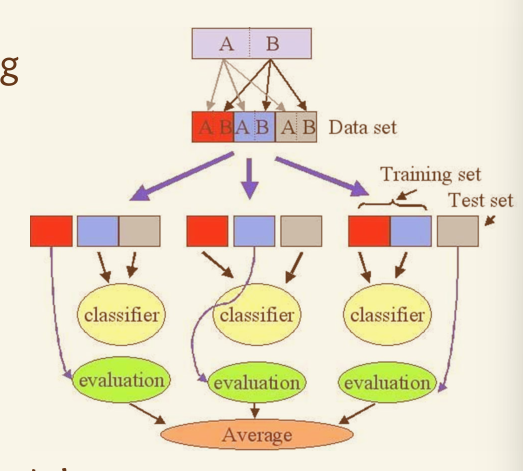
优点：

• 各次评估结果的平均值可以更准确地反映模型性能。
• 更稳定，评估结果不依赖单次数据划分。

缺点：

• 计算开销较大，尤其是数据集较大时。

第06章-支持向量机

#

SVM 概念

#

三种分类：

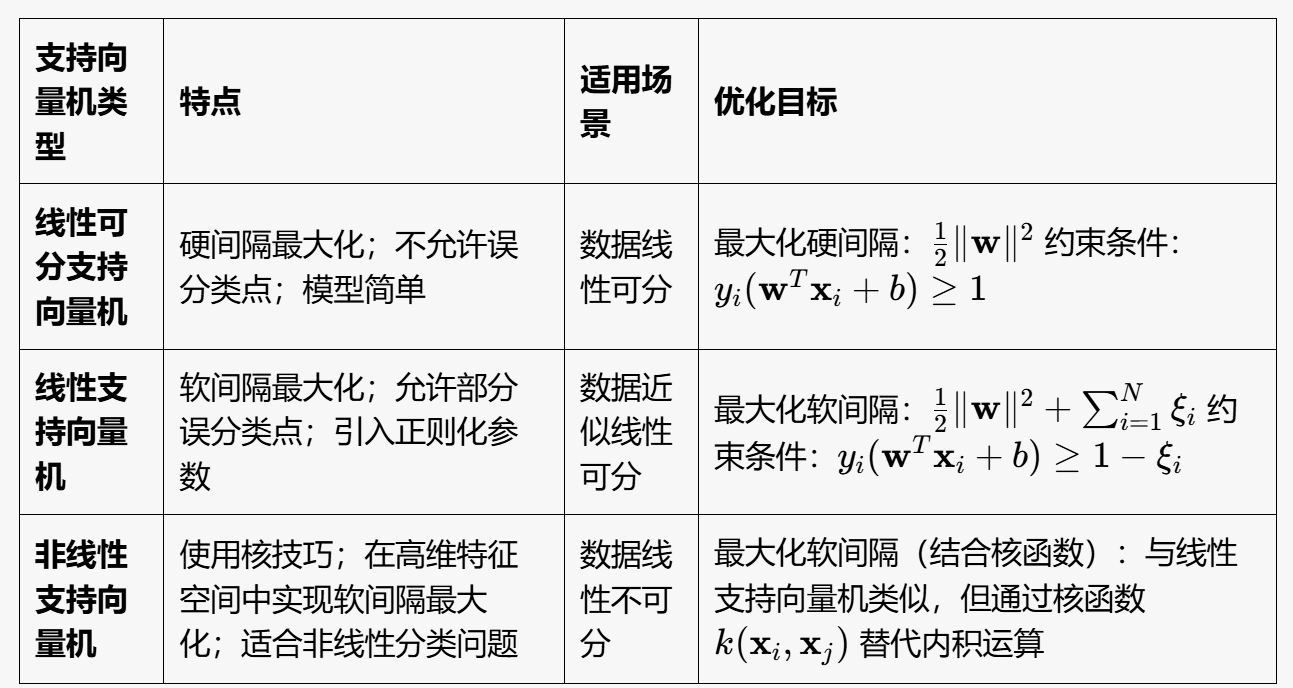
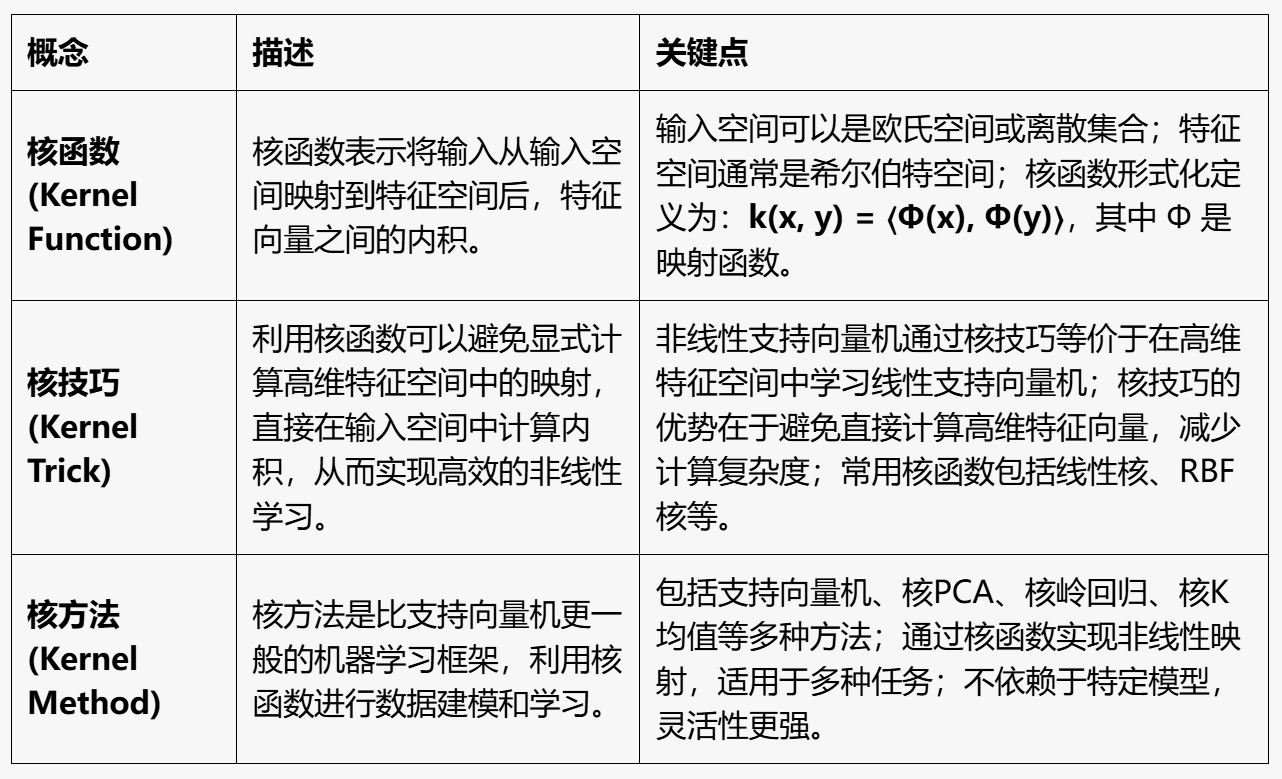
核函数、核技巧、核方法：

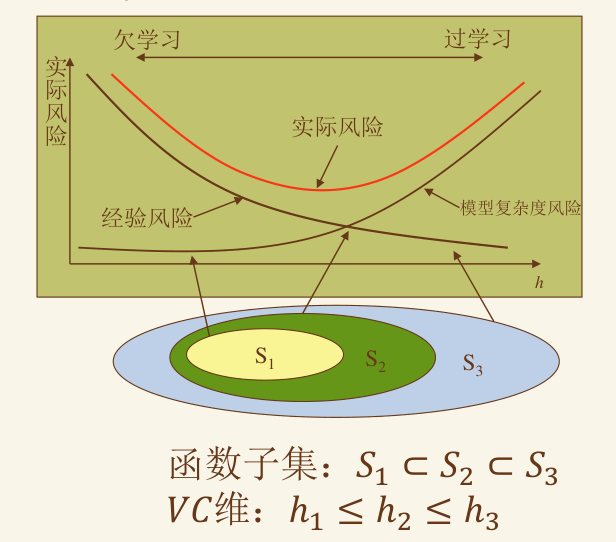
SVM 如何克服过拟合

#

线性可分 SVM — 硬间隔最大化

#

线性 SVM — 软间隔最大化

#

非线性SVM — 核技巧

#

回归问题 SVR

#

在Support Vector Regression(SVR)中，同样也是计算间隔，不同的是使靠超平面最远的样本点之间的间隔最小。

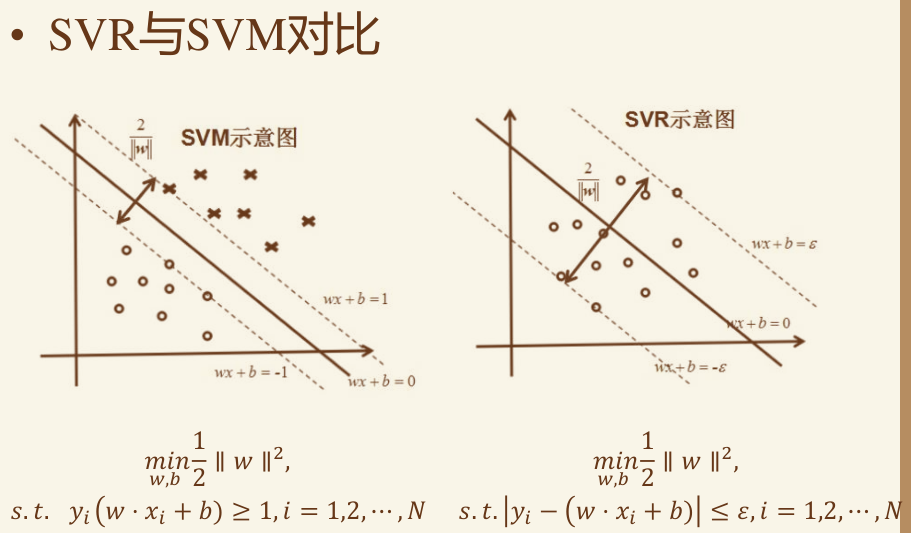
仅仅是约束有所不同

第07章-聚类

#

聚类（Clustering）是最常见的无监督学习算法，它指的是按照某个特定标准（如距离）把一个数据集分割成不同的类或簇，使得同一个簇内的数据对象的相似性尽可能大，同时不在同一个簇中的数据对象的差异性也尽可能地大。

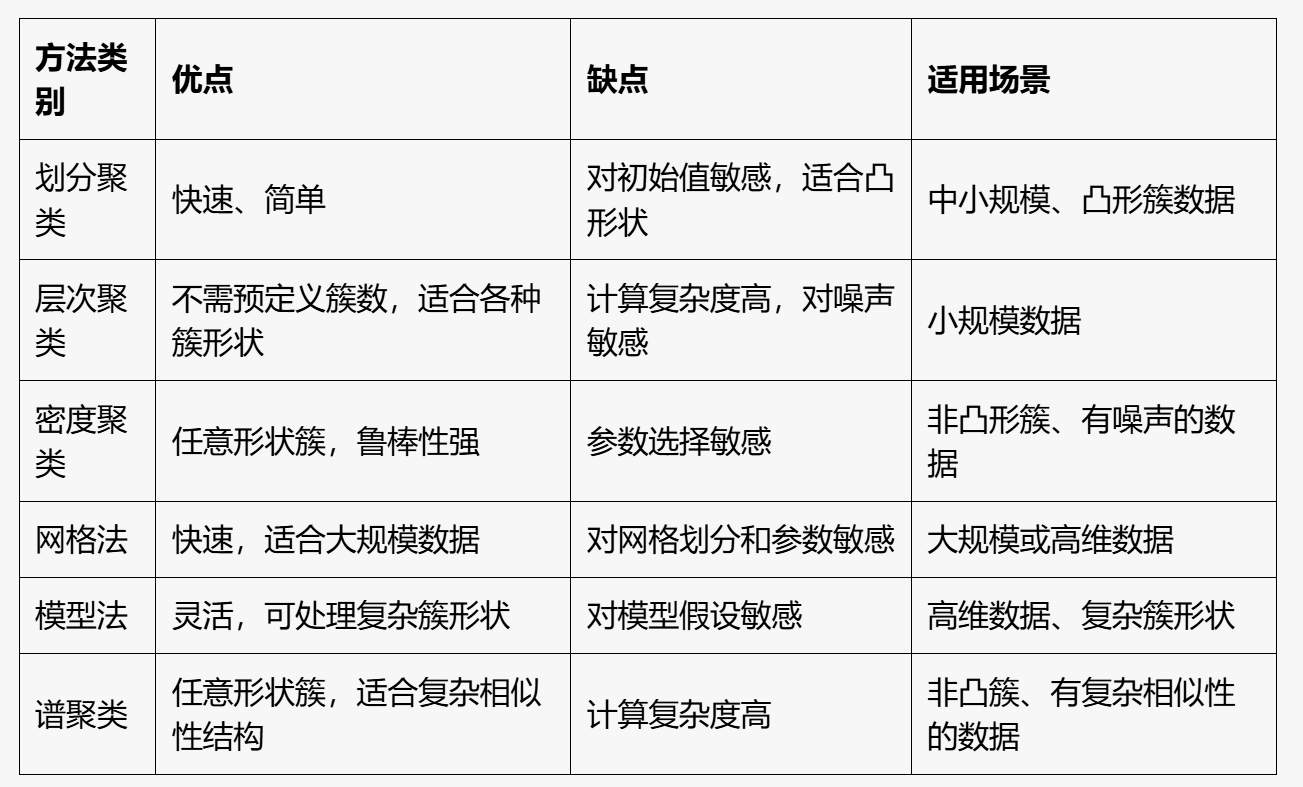
主要类型

#

◼ 划分聚类（K-means、K-medoids等）

◼ 层次聚类（凝聚法、分裂法）

◼ 密度聚类（DBScan、基于密度峰值算法）

◼ 网格法（STING、CLIQUE）

◼ 模型法（概率模型：高斯混合模型Gaussian Mixture Models ；神经网络模型:SOM；吸引子传播算法： AP聚类）

◼ 谱聚类

划分聚类

#

• K-means：通过最小化簇内点到簇中心的平方误差，将数据划分为 k 个簇。
• K-medoids：簇中心是数据点本身，通过最小化绝对距离实现聚类。

---

层次聚类

#

• 凝聚法：从每个点作为一个簇开始，逐步合并最相似的簇。
• 分裂法：从所有点作为一个簇开始，逐步将簇分裂成更小的簇。

---

密度聚类

#

• DBSCAN：通过核心点的密度连接形成簇，能够发现任意形状的簇。
• 基于密度峰值算法：通过识别局部密度的峰值作为簇中心实现聚类。

---

网格法

#

• STING：将数据划分为网格，并基于网格的统计信息进行聚类。
• CLIQUE：结合网格划分和密度聚类，能够发现高维空间中的稀疏簇。

---

模型法

#

• 高斯混合模型（GMM）：假设数据由多个高斯分布组成，用概率计算点的簇隶属关系。
• SOM：通过神经网络将高维数据映射到低维空间，同时保留数据的拓扑关系。
• 吸引子传播（AP聚类）：基于数据点间的相似性，通过消息传递选择簇中心。

---

基于网格的聚类

#

• 将数据空间划分成有限个单元的网格结构，所有的处理都是以单个的单元为对象

K-means算法

#

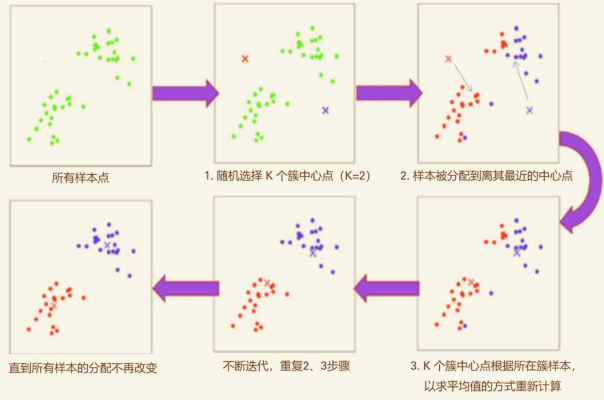
K-means 算法的流程

#

1. 随机选择 K 个簇中心点（可以选已有的数据作为中心点，也可直接选高维空间中的位置）

2. 样本被分配到离其最近的中心点

3. K个簇中心点根据所在簇样本，以求平均值的方式重新计算

4. 开始迭代，重复第2步和第3步直到所有样本的分配不再改变

   

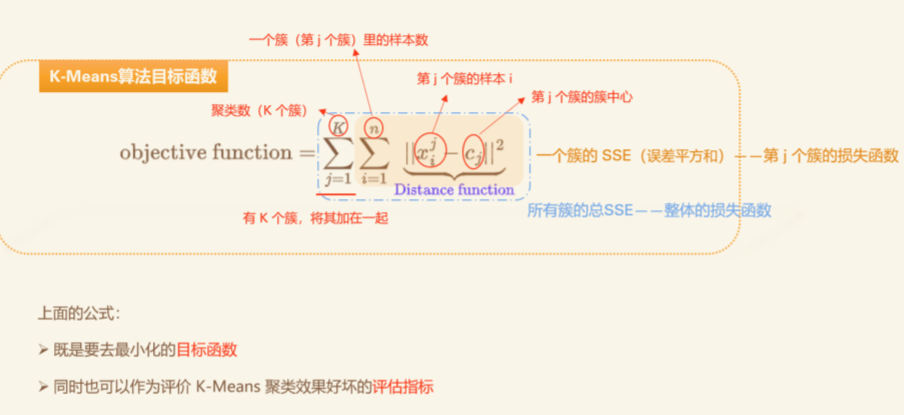
损失函数

#

K 的选择

#

K-means算法 K 的选择(肘部法（elbow method）) • 目标：找到最合适的点——拐点 • 找到一个聚类数目，使得 K 高于该值之后的**损失（即上面的损失函数）**的变换会发生显著递减；也就是该点后的 loss 变换开始不明显。 • 这个 K 值，称为肘部点（elbow point），因为它看起来像一个人的肘部。

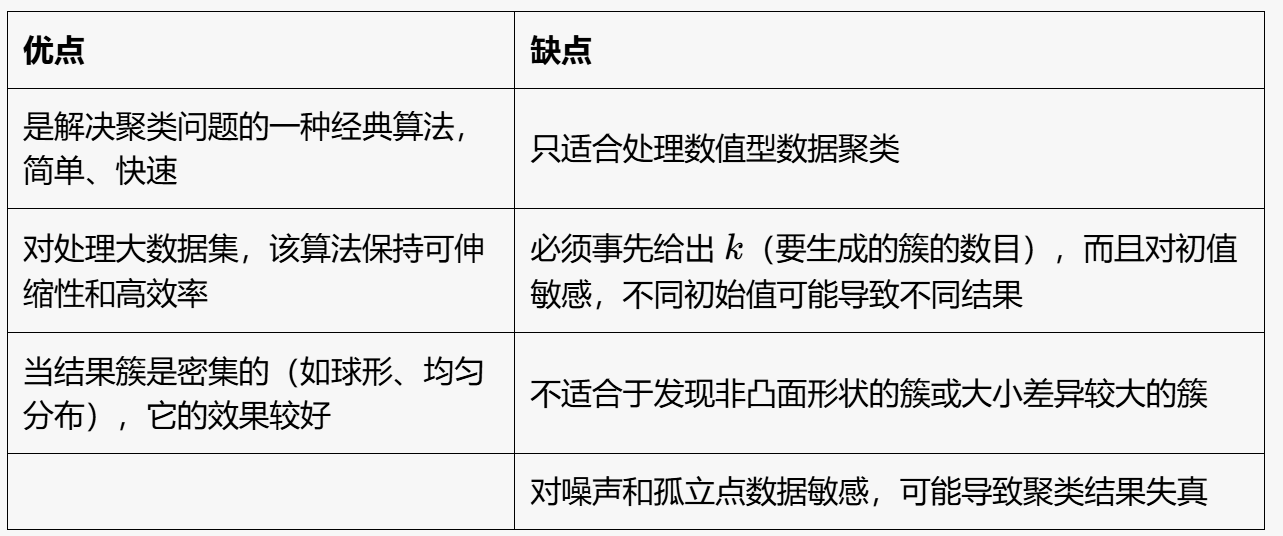
优缺点

#

第08章-降维

#

维数灾难(Curse of Dimensionality)：通常是指在涉及到向量的计算的问题中，随着维数的增加，计算量呈指数倍增长的一种现象。

在很多机器学习问题中，每条数据经常具有很高的特征维度。如果直接使用原始的数据，不仅会让训练非常缓慢，还会影响模型的泛化性能。

降维(Dimensionality Reduction)是将训练数据中的样本(实例)从高维空间转换到低维空间。该过程与信息论中有损压缩概念相似，完全无损的降维是不存在。

降维方法又分为线性降维和非线性降维，非线性降维又 分为基于核函数和基于流形等方法。

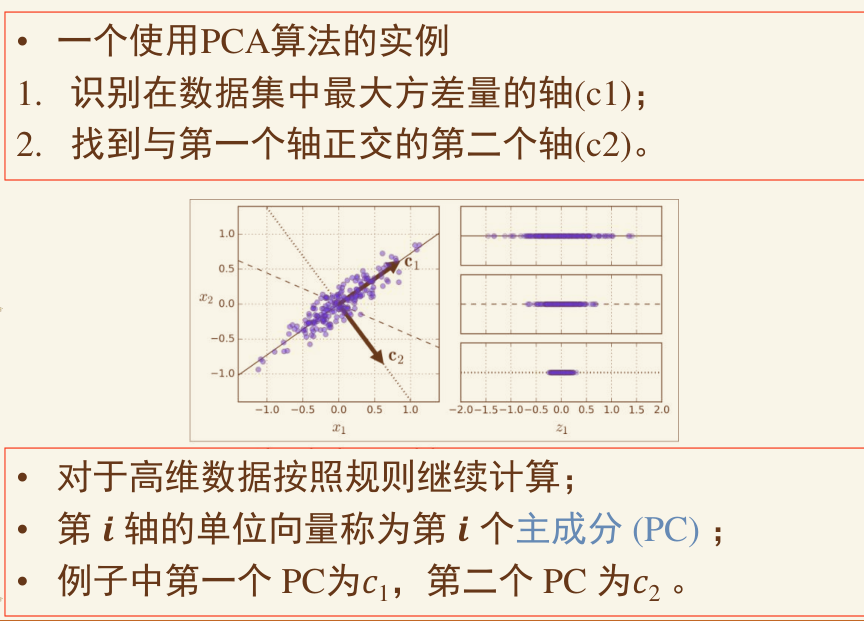
PCA

#

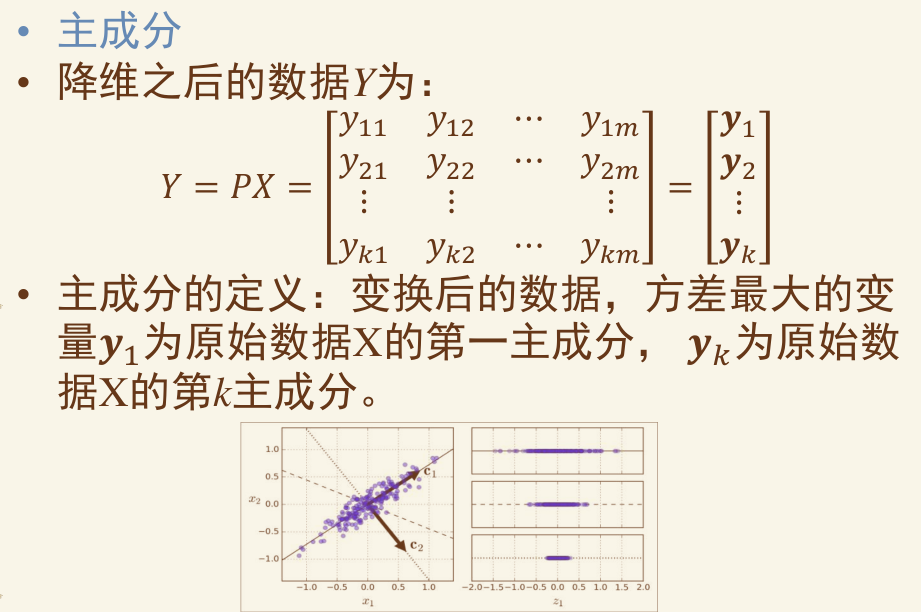
通过平移、旋转坐标轴完成对数据原始特征空间的重构

PCA算法对于重构和降维的要求：

1. 重构的不同维度之间线性无关(正交、协方差为0)；
2. 降维后所得维度的值尽可能分散(最大方差)；

考试复习重点

#

• PCA计算（必考）
  1. 条件：X矩阵 -> 减去 μ -> 其中可以是 m 或 m - 1 有 C = 1 / m * (X @ X.T)求协方差矩阵
  2. 协方差矩阵 -> 求特征值或特征向量（一般很难求，除非设计好数据）
  3. 特征向量转置则为 P，有P @ C @ P.T = λ 主对角线矩阵
  4. 降维 Y = Pi @ X ，贡献度为 λi 在 Σλ 的比值
• SVM 给三个点求超平面
  1. 一定是三个点，因为三个点以上需要用SMO迭代
  2. 直接给对偶式子以及其st
  3. 带入即可求 a1 a2 a3
  4. 由 w = Σayx 得 w，带入任何一点即可求得 b
• 用正规方程求解线性回归
  1. linalg.inv(X.T @ X) @ X.T @ Y
  2. 其中难点在求逆矩阵，增广矩阵法（会考吗？）

证明题：

#

• 最小二乘法的关键因子推导（最简单）+ 带入梯度下降公式

• 最小二乘法的正规方程推导

• 线性回归最小二乘法的概率解释

• 逻辑回归极大似然估计公式推导 -> 与线性回归的形式一致性

• 线性可分 SVM

  1. 从距离推导到目标
  2. 拉格朗日乘子法
  3. 求解 max (min L)
  4. SMO （非重点）

• 软间隔SVM 、非线性SVM 、SVR 推导可能性较小

• BP算法 （非重点）

论述题：

#

• 大概率一道回归、一道分类

• 回归可能的点：

  1. 房价预测实例
  2. 维度灾难时使用降维
  3. 最小二乘法为什么自然
  4. 非线性回归问题 -> 神经网络、SVR、线性回归核函数
  5. 分出训练集 测试集 验证集
  6. 正则化与过拟合

• 分类可能的点：

  1. 区分有监督分类和无监督聚类

  2. SVM的使用方法、逻辑回归的使用方法（梯度与牛顿）

  3. SVM相比逻辑回归的好处

  4. 神经网络的分类任务？

  5. 二分类效果评估方法 F1 等

简答题、选择题：

#

• 监督学习 vs 无监督学习

• 符号主义、连接主义、统计

• 线性回归与逻辑回归中的 X 矩阵实际上是增广矩阵，用于适配 wx + b 中的 b

• 损失函数 = 代价函数 ；加上 min，max 为目标函数

• 特征规范化：x1=(x1-mean(x1))/std(x1)

• 梯度下降与梯度上升（爬山）

• 学习率的选择问题，过大会怎么样，过小会怎么样

• BGD vs SGD vs mini-batch

• 全局极小值 vs 局部最小值

• 线性回归 梯度下降 vs 正规方程

• 过拟合与欠拟合 + 正则化

• 什么是分类问题（硬分类与软分类），什么是回归问题

• 单位阶跃函数 vs. Sigmoid function

  • Sigmoid 好在哪？，其参数怎么控制形状

• Odds(几率、几率比)、似然函数

• 牛顿法 vs 梯度法 牛顿法定义

• 训练集 测试集 验证集

  • 交叉验证、K=10、留一法
  • 自助法，可重复采样

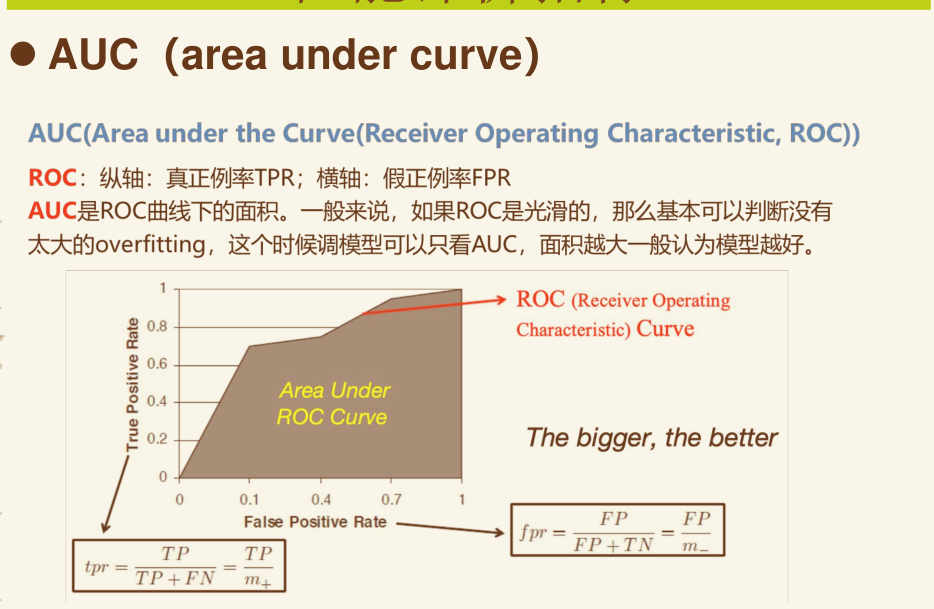
• 准确率 精确率 召回率 F1score AUC

• 核函数 核技巧 核方法

• 结构风险最小化

• SVM 硬分类、软分类的 Margin 定义（松弛因子）

• 非线性 SVM 的 𝐾(𝑥, 𝑦) = φ(𝑥) ⋅ φ(𝑦) 与 φ(x) : 𝑋 → 𝑅𝑚 (𝑚 ≫ 𝑛)

• 高斯核参数以及惩罚参数对于分类情况的影响

• KKT 强对偶

• SVR 定义，目标函数

• 聚类问题定义

• 划分聚类：K-mean算法具体步骤与公式

  • 肘部法选择 K
  • 优点缺点，对初值敏感
  • 改进算法

• 层次聚类 密度聚类 网格法 模型法 谱聚类的定义

• 什么是降维，什么是维度灾难，为什么降维

• 完全无损的降维是不存在

• PCA的思想（计算考了，这里不考）

  • PCA要求：正交（协方差为零）和最大方差

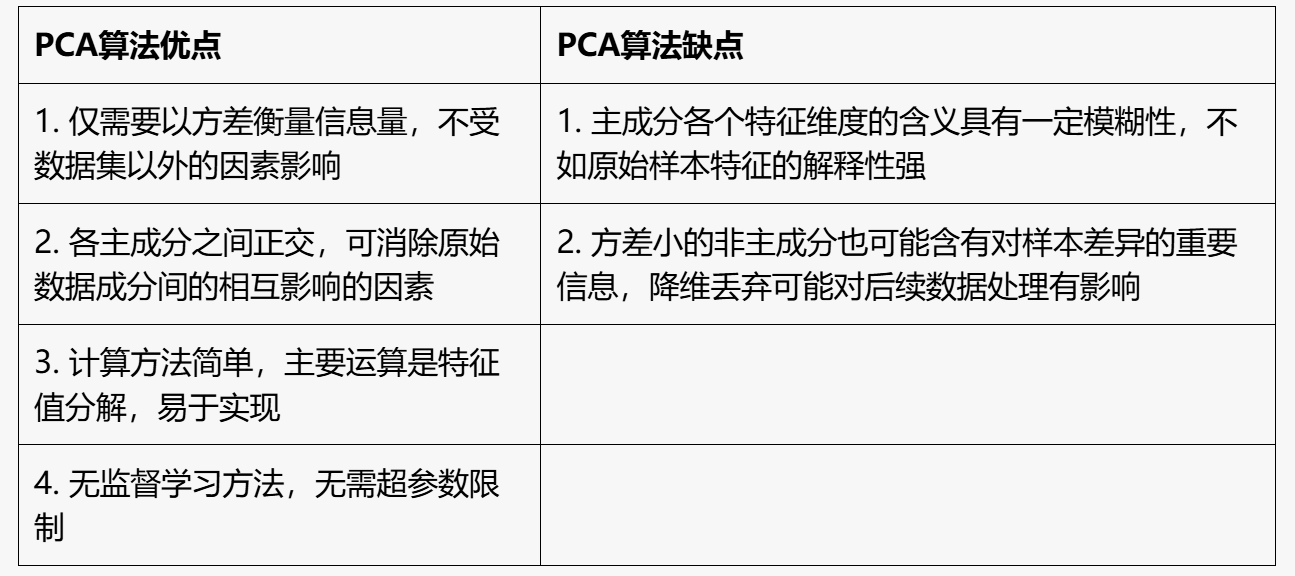
  • PCA的优缺点

• 神经网络 与 RBF神经网络

• 感知器定义 感知器的表征能力

• 多层前馈网络 正向传播 + 反向传播

考试数学推导重点（手写）

#